数理工学 (mathematical engineering)，応用数学 (applied mathematics)．
工学の中に潜んでいる数理を見つけ出し，既存の数学を駆使して，あるいは必要なら新しい数学を作りだして，問題を解く方法を考えていく学問です． 数学はもちろんのこと，種々の工学，物理学・化学・生物学・経済学，計算科学などと広い交わりを持ちます． （数理工学／数理情報学専攻紹介ページも参照してください）
個人的には，より詳しく言うと，数値解析学，特に微分方程式の Geometric Integration を専門としています． (→業績一覧，も参照してください)．
下に，いくつか研究テーマを挙げます．
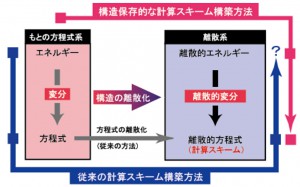
- Geometric Numerical Integration：「幾何学的数値解法」とか「構造保存数値解法」などとも呼ばれます．微分方程式の数値解析学における，一つの学問分野です．
そもそも微分方程式の数値解析は，Eulerの時代から（計算機がない時代から！）研究がある非常に古い学問分野で，常微分方程式に対するRunge-Kutta法，偏微分方程式の対する差分法，有限要素法など，色々な解法が生み出され研究されてきました．特に常微分方程式に対しては，Dahlquist，Butcherらにより整然とした研究が行われ，1980年代にはかなり成熟した体系が完成されています．この種の解法は，特に対象とする常微分方程式を限定しない，いわゆる「汎用解法」と呼ばれるものです．
この汎用解法の限界を超えるために，研究者達は次に「問題を限定する代わりに，汎用解法を超える解法を作る」試みを始めます．この種の専用解法は，実は1980年代に初めて生まれたものではなく，天文学や分子動力学などの分野で，物理学者達によって「ある特定の問題に対して，すばらしくよく動く」数値解法の存在は古くから知られていました．多体問題に対するStoermer-Verlet法などです（実に，100年以上前に既に発見されていたアルゴリズムです！）．ここで述べる，1980年代に起こった新しい動きとは，そういった特殊な数値解法がうまく動く理由を数学的に理解して，「そのアイデアが有効な問題クラスの特徴付けと，数値解法群の整備」を行うものでした．先に述べたStoermer-Verlet法は，いまでは「symplectic数値解法」と呼ばれる数値解法群のひとつで，Hamilton系のフロー（時間発展写像）が持つsymplectic性を離散系でも再現する解法である（それゆえにHamilton系に対して，汎用解法よりも遙かにうまく動く）ことが理解されています．
以上は常微分方程式の場合ですが，偏微分方程式に対する研究は，10年ほど遅れて1990年代に始まっています．その黎明期を支えたグループのひとつが，我々日本人チームで，日本初の手法である「離散変分導関数法」（Discrete variational derivative method；DVDM）は，偏微分方程式に対する強力な構造保存数値解法として世界的にも認知されています．DVDMは，当時東大工学部６号館（物理工学科）にあった数値解析グループ（降籏・森）によりその原型が提案され，その後松尾も加わって，以降20年ほどに渡り集中的に研究・発展されてきました．この研究分野における松尾の主な仕事は，- 非線形Schroedinger方程式など複素数値偏微分方程式の取り扱い定式化と，一部スキームの理論解析（離散関数解析）
- 陰的線形化手法の導入（＝高速化の導入）
- Camassa-Holm方程式などの非局所偏微分方程式の取り扱い定式化
- もともと差分法をベースに構築されたDVDMの有限要素法版，不連続Galerkin法版の構築
などです．（もちろん，ひとりでやったわけではなく，学生さんを含む様々な協力者がいます．）
以上の仕事は，共同研究者の降籏大介氏（大阪大学）と共著の洋書にもまとまっています（2011年）．
DVDMは，ひと言で言えば，数学的にある種の無限次元勾配系とみなせる偏微分方程式群に対して，その勾配構造を離散版でも再現することで，その方程式に特化した数値解法を作り出す手法です．このような解法を用いると，勾配構造に由来する方程式の数学的特徴量（保存量やLyapunov関数）が離散版でも再現され，それゆえに，より定性的に適切な数値解が得られることになります．（このように，方程式の幾何学的構造を抽出して数値解法を構成するので，「幾何学的数値解法」とか「構造保存数値解法」と呼ばれます．）
左の図は，DVDMの概念図です．この研究の流れで，まだまだ知りたいことがたくさんあります．それらについては，項を改めて下に列挙します．
- 力学系理論を用いた多段階法の安定性解析と安定化：松尾がいま一番興味を持っているテーマです．
上で，「DVDMにおける陰的線形化手法」という仕事に触れました．これは，ひと言で言えば，非線形偏微分方程式に対して，多段化（＝計算公式が３つ以上の時間ステップに跨がること）を許すことで，計算公式が非線形になることを防ぎ，従って，時間発展にあたり，計算コストの重いNewton法などの反復解法を不要にする技法です．これは大変うまくいっているのですが，多段化に自由度があり，「うまい多段化を選ばないと計算公式が不安定になる」ことが分かっています．しかし，この「うまい多段化」が分からないのです．自由度を，（職人の勘に従って！？）順番に試してみて，安定に動くものを探すしかないのです．
「安定な多段化を自動的に選び出す指導原理はないのか？」——松尾らの，上の線形化が公開されてから，他国の研究者達もこの興味深い問題にアタックしましたが，この文章を書いている現在，いまだこの問いの答えはopenです．
松尾も，この問題は難しいな．．．と思い，しばらくあきらめていました．が，2011年頃，「そもそも，安定に動いているものがなぜ安定なのかを理解していないのだな」ということに気がつき，力学系の理論（ω極限集合とLyapunov関数）を使って，まず，易しい常微分方程式の問題に対してそれを理解してみることを始めました．これは案外うまくいって，非常にきれいに物事が理解できることが分かりました（Matsuo-Furihata, 2014）．
いまは，この「続き」に興味をもっています．最終的なゴールは，偏微分方程式に対して，漸近挙動の完全な制御を含めた安定化手法（指導原理）を確立することです．それにあたり，連続系のLyapunov理論と，離散写像のLyapunov理論のどちらでもない，「連続系の近似としての離散写像群に対するLyapunov理論」を作らねばならないと漠然と思っています．援軍募集中です．
いま，幸い，数理３研には力学系のプロである鈴木秀幸准教授がいらっしゃるので，ぜひ協力して色々研究してみたいと思っています． - 空間２，３次元の偏微分方程式に対して構造保存解法は本当に有効か？：これもずいぶん前から興味をもっていて，計算機に強い学生さんが来るたびに，トライしているテーマです．
上で，構造保存解法を大変持ち上げましたが，世の中の良いものには常にコストがついてまわるもので（これを英語では “There is no free lunch.” と言います．言い得て妙ですね！），高速な汎用解法と比べると，計算速度の点ではどうしても劣ります．それも，しばしば，激しく劣ります．残念です．構造保存解法は数値解の定性的挙動がかなり優れているので，長時間微分方程式を積分すればいずれは汎用解法に勝ってくるのですが，その「いずれ」がどの辺なのかが問題です．いまは，この「いずれ」はかなり遠くであろう，と悲観的に思われています．
このあたり，実際問題としてどうなのか？色々な偏微分方程式で試してみて知りたいと思っています．このテーマは上の項目とリンクしていて，どういう多段化（高速化）を施すのがよいのか？も研究の対象です．また，同じ数理３研にいらっしゃる中島研吾先生がご専門の，いわゆるHPC（High Performance Computing）技術との相性も，そろそろ本気で考える時期で，そういった方面にも切り込んでいきたいと思っています．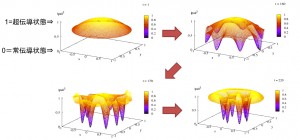
右の図は，超伝導現象を記述するGinzburg-Landau方程式に有限要素法版のDVDMを適用してみたものです．円盤状の超伝導体（２次元）の上に，「渦点」が発生する様子がよく見えます．この計算は不安定になりがちですが，DVDMを用いると，かなり大きな時間刻みでも安定に計算できます．が，このレベルの２次元の計算でもプログラミングと計算はかなり大変です． - 構造保存数値解法における新しい問題クラスの発見：偏微分方程式に対しては，上述のDVDMに代表される「無限次元勾配系に対するもの」，multi-symplectic法と呼ばれる「無限次元Hamilton系に対するもの」が，２大手法（および問題クラス）になっています．これ以外のものは，あまり知られていません．
しかし偏微分方程式は非常に種類が多く，上の２つのクラスに入らないものがたくさんあります．そういったものをうまく分類して，新しい幾何学的対称性をくくり出すことはできないか？そしてそれをうまく離散化することはできないか？それを考えてみるべきです．
また，少し問題は変わってしまいますが，この「問題の対称性をうまく抽出して，それを活かした数値解法を作る」というのは，微分方程式に限らず，数値解析の幅広い分野で有効なはずです．例えば対称行列の固有値問題は，対称性をうまく活かして解く方法が考えられており（Jacobi法やMRRR法など），これは，そうは呼ばれていませんが，「構造保存数値解法」の属性を持つ手法であると言えます．これを延長して，より高度な（稀な）対称性を狙い撃ちする線形計算手法もありうるのではないでしょうか？例えば，特殊な物理の問題から出てくる固有値問題では，係数行列が何らかの物理的対称性を反映した形をしているはずで，それを崩さないように固有値を求める，というのは自然な考え方で，物理屋さんの考えた個別研究もあるはずです．それを数学的に昇華させることは興味深い研究テーマです．—以上が，構造保存数値解法に関連するテーマです．ここから下は，それ以外にこれまでに扱ったことのあるテーマ，およびこれから興味を持っているテーマです．—
- 関数近似，特にSinc数値計算法：（杉原正顯先生（青山学院大学），岡山友昭氏（広島市立大学）らとの共同研究）
関数近似は数値微分，数値積分など，多くの解析系数値解析の源流となる理論です．関数は一般に無限次元空間に属し，それを（計算機に載せるために）どう有限次元近似するかは自明ではありません．被近似関数のクラスごとに最適な近似法が研究されており，科学・工学が進化して新しい問題が出てくるごとに，常に新しい関数近似が考えられています．
Sinc関数（sin(x)/x）は，解析関数の近似にとても向いていることが知られています．特に，日本発の強力な手法である「二重指数関数型変換」（高橋・森）と相性が良く，それと組み合わせたSinc数値計算法は，微分方程式，積分方程式など，様々な問題に対して強力なツールとなることが分かっています．これを，新しい問題へと展開していくことが望まれています． - 線形計算（特異値分解など）：（相島健助氏（数理３研助教），杉原正顯先生（青山学院大学），室田一雄先生（数理２研）らとの共同研究）
「線形計算」とは連立一次方程式，固有値問題，特異値問題，最小二乗問題などの計算法を考える分野で，「あらゆる数値解析は線形計算に落ちる」と言われるくらい基本的です．連立一次方程式なんて解くのは簡単だ，と思うかもしれませんが，- 計算機では非常に解きにくい連立一次方程式（＝係数行列）が存在する
- 最先端の科学技術計算では気が遠くなるほど大きな連立一次方程式が解かれており，それをどうやって高速に解くかは自明ではない
などの理由から，現在でもまだ盛んに研究が行われている分野です．ただし研究の歴史の古さから，研究者の細分化・職人化が進んでおり，なかなか新規参入がしにくい分野でもあります．
それでも，アイデア次第で新しい研究もできます．相島らによる一連の研究では，特異値分解アルゴリズムのdqds法の漸近収束性を新たに理論的に証明することに成功しました（Aishima-Matsuo-Murota-Sugihara, 2008など）．この証明は，既存の証明よりも簡明で，かつすべての要素の漸近挙動を明解に記述するもので，この研究を端緒に，様々なアルゴリズムの漸近挙動の研究が一斉に始まりました．
同様のことはこれからも起こりえます．日々進歩する線形計算アルゴリズムを注視して，新しい研究の種を探したいと思っています． - テンソルに対する数値計算法：これはこれまでに私自身の成果はなく，これからのテーマとしていま興味を持っているものです．
機械学習など現在流行している学問分野で，巨大なテンソルを扱う機会が増えてきています．ここで言うテンソルは（物理学で言うところのテンソル場のテンソルではなく）「行列は２次元配列データ」と思ったとき，３次元以上の配列データのことを指します．この「次元」のことを一般に「オーダー」と呼びます（従って行列は「オーダー２のテンソル」です）．オーダーが上がればデータ量は必然的に増えていくため，それをどう効率よく計算に用いるか，特に行列で言うところの特異値分解に対応する分解をどう行うかは大きなテーマです．（分解ができれば，それに基づくデータの圧縮ができます．）
当然ながら，この種の研究はすでにされていますが，主に機械学習などの分野の人たちが主役であって，これまで古典的数値解析学の学者たちは，あまりその舞台に参戦してこなかったように思います．しかし，数値解析学者の視点から見た研究もなされるべきです．
いま松尾の研究室では，いくつかのテンソル分解アルゴリズムの性能評価と，それに基づくアルゴリズム改良の研究を始めています．
