私の研究室を志望する学生の方へのメッセージです．

私の専門は数値解析です．「数値解析」（numerical analysis）とは聞き慣れない言葉かもしれませんが，ひと言で言えば「シミュレーション時代の基礎科学」である，と私はよく言っています．

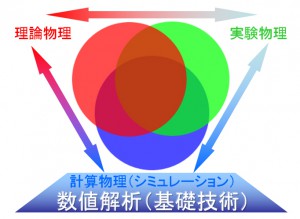
一つわかりやすい例を挙げます．物理学は，そもそも「理論物理」と「実験物理」が協力し合って発展してきました．例えば理論物理が現象を予言し（アインシュタインの重力レンズなど），反対に，実験が理論を示唆したりです（黒体輻射と量子力学の発見など）．数十年前から，そこに「計算物理」という新しい軸が加わり，いまでは「理論・実験・計算」の３者が軸である，という理解が標準的だと思います．「計算物理」とは，計算機の中で物理現象を実験してみることで，宇宙黎明期の銀河形成シミュレーションや宇宙船の風洞実験などが挙げられます．理論（紙と鉛筆）だけでなかなか切り込めないところ，あるいは実験したくても地上では難しいものを，計算機を使って調べてみる分野です．

物理学に限らず，いまはこの種の「計算＊＊」という学問が，現代科学・工学のあらゆるところで標準的になっています．そのすべての分野の基礎となるのが数値解析技術であり，数値解析学の理論です．この意味で，「数値解析は，シミュレーション時代の基礎科学」なのです．

「計算なんて，計算機を買ってくれば誰でもできるのでは？」そう思う人も多いと思います．しかし，実は，中学生にも解ける問題が，計算機では解けないということも起こるのです．その典型例が連立一次方程式で，こんなものは中学生でも（原理的には）解けるものですが，いざ計算機で解こうとすると解きづらい問題（→行列の条件数），あるいはそもそも次元が莫大に大きすぎて，うまい方法で計算しないと時間がかかりすぎる問題などがあり，実はいまだに「連立一次方程式の数値解法の決定版（これだけ使えば世の中幸せな解法）」は存在していません．そんなものはないのではないか・・・という悲観論もないわけではないくらいですが，しかし，数値解析学者は次世代の科学・工学の基礎を確立するため，日々奮闘しています．その挑戦に参加してくれる若者を歓迎します．

数値解析は，「応用＝どういう問題を計算してみたいか」，「計算機＝どういう計算機で計算してみたいか」，および「数学＝どういう数学を使って問題・アルゴリズムを考えたいか」の３分野に跨がる分野です．そのどれかに興味があれば，そこを切り口に研究ができます．

• 物理や○○工学など応用分野にバックグラウンドがあるが，そこで行われるシミュレーションをもう少し数学的に掘り下げて考えてみたい人
• 具体的な応用問題には興味はないが，最先端の数値解析アルゴリズムに興味があり，参戦してみたい人
• とにかく計算機を回してみたい人

色々入り口はありますので，まずは相談にきてみてください．「応用・計算機・数学」，そのどれもに強いと理想的ですが，プロでもなかなかそういう人はいません．どれかひとつでも強みがあればそれで十分です．強いて申せば，「計算をしない数値解析研究」は難しいので，プログラミングはある程度できた方がよいですが，これは修士に入ってから先輩のプログラムを見たりして覚えればそれでも十分です．

なお，私が所属する数理情報学専攻は，そもそも数学志向の人が多い専攻です．その人達向けに，数値解析の数学的な面白さについてもう少し言及しておきます．

「数値解析」とはなにか．上で「シミュレーション時代の基礎科学」という標語を挙げましたが，数学の観点から申せば，「数学と計算機を結ぶ試み」であると言えると思います．数学の計算を計算機の中で実行するのが「数値計算」なわけですが，これが一筋縄ではない，ということは上にも書いたとおりです．「丸め誤差」やらなにやらがあって，ノートの上に書いた数式のとおりには計算が進行しないからです．

と書くと，「数値解析学者は誤差＝ゴミを回収して回る掃除人」のように聞こえてしまうのですが，少し数学的な言い方でこれを言い直してみます．実は，計算機の中の「世界」は数学的には壊れているのです．

• そもそも計算機の中の「数の空間」は線形空間ですらない： 教養で習う数学は，「まず線形空間というのがあってね」というところから始まります．ところが計算機の中の数は，「浮動小数点数」という離散化された値しかとれず，一般に浮動小数点数の和は（同じ体系の）浮動小数点数では表せません．つまり，「浮動小数点数の集合」は線形空間をなしていないのです．このことの帰結が「丸め誤差」です．
• 計算機には有限の呪いがかかっている： もうひとつの計算機の欠陥は，「有限性」です．数学，特に解析学では極限操作が基本的です．微分演算ひとつとっても極限が要りますし，また関数空間を考えればそれは当然無限次元になるわけですが，この種の無限性は，有限の操作・有限のメモリしか許されない計算機では本質的に考えられません．これを正直に捉えれば，計算機の上では解析学は再現不可能ということになります．

以上，こんな基本的なところから，計算機の「世界」は数学的に壊れているのです．にも関わらず，もはや我々は数値計算抜きでは生きられず，その壊れた世界で数学をすることを強要されるのです．このことを苦痛と思うか，やり甲斐のある挑戦だと思うか．もちろん，すべての人がこれを「楽しい」と思えるわけではないでしょう．私だって，常に何もかも面白いと思えているわけではありません．ただ，多くの場合，この欠陥は工夫により乗り越えられる．それもしばしば，数学的な工夫によって乗り越えられます．

例えば，私が専門とする微分方程式の数値解法では，「無限」が必要な微分方程式を「有限」の操作だけで解くわけで，時間発展するごとにどうしたって「正解＝無限」から離れていくのは，本質的にどうしようもないことです．でも，方程式の幾何学的対称性を取り込んだ賢い解法（これを「構造保存数値解法」と言います→私の「研究」のページをみてください）を考えることで，その乖離を遙かに小さくできます．

つまり，計算機の中で壊れてしまった数学の世界を救うのも，また数学なのです．そのことを面白いと思ってくれる人は，数値解析に向いている可能性があります．